Die Beweglichkeit der Schachfiguren
In den 1960er Jahren, als das Computerschach noch in den Kinderschuhen steckte, lud ein Kollege an der Universität Stuttgart mich ein, an dem von ihm geleiteten Recheninstitut gegen den Computer eine Partie Schach zu spielen. Denn einer seiner jungen Mitarbeiter war dabei, ein Schachprogramm zu entwickeln, und beide wollten nun dieses Programm an einem Testspieler von mäßiger Spielstärke wie mir erproben.
Vor der Partie ließ ich mir ein wenig erläutern, wie das Programm konzipiert war. Vereinfacht ausgedrückt, war die Idee etwa folgende: Vor jedem Zug wird virtuell eine vollständige Liste aller Züge aufgestellt, die in dieser Stellung möglich sind. Auf diese Liste werden in einer bestimmten Reihenfoge nacheinander 14 Auswahlkriterien angewandt, bis am Ende ein einziger Zug übrig bleibt, den das Programm dann ausführt. Die ersten paar Kritierien lauteten, grob gesagt, in der Reihenfolge etwa so: Wenn du in den nächsten Zügen forciert den Gegner mattsetzen kannst, dann tue es. Wenn der Gegner eine Mattdrohung hat, dann verteidige dich dagegen. Wenn du in den nächsten Zügen (per Saldo) Material gewinnen kannst, dann tue es. Vermeide Züge, die zu Materialverlust führen. Nach solchen Kritierien folgten dann solche über Eröffnung, Figurenentwicklung u.dgl. Danach folgten Kriterien für Mittelspielstellungen ohne taktische Besonderheiten. Sie liefen darauf hinaus, den Computer immer zu einenm Zug zu veranlassen, der die Gesamt-Beweglichkeit der eigenen Figuren so weit erhöht wie möglich. Damit ist die Anzahl der Zugmöglichkeiten gemeint, die der Computer hätte, wenn er anschließend (statt des Gegners) selbst nochmals am Zug wäre.
Dieses Kriterium ist gerade für den Anfänger gar nicht so schlecht. Wenn man z.B. die Ausgangsstellung bestrachtet, so beträgt die Gesamt-Beweglichkleit für Weiß offenbar 20. Denn ihm stehen (theoretisch) 20 Züge zur Wahl, nämlich vier Springerzüge (Sa3, Sc3, Sf3, Sh3) und 16 Bauernzüge (a3, a4, b3, b4, ..., h3, h4). Dabei ist es schachpädagogisch interessant, dass das Programm nach diesem Kriterium unter den 20 erwähnten Zügen tatsächlich den gebräuchlichsten Eröffnungszug 1. e4 wählen würde. Denn durch diesen Zug erhöht Weiß seine Gesamt-Beweglichkeit von 20 auf 29, weil er anschließend, wenn er nochmals am Zug wäre, unter folgenden 29 Möglichkeiten wählen könnte: Ke2, De2, Df3, Dg4, Dh5, Le2, Ld3, Lc4, Lb5, La6, Sa3, Sc3, Sf3, Sh3, a3, a4, b3, b4, c3, c4, d3, d4, e5, f3, f4, g3, g4, h3, h4. Die übrigen 19 möglichen Eröffnungszüge führen alle auf kleinere Werte als 29. Z.B. erhöht der Zug 1. d4 die Gesamt-Beweglichkeit von 20 auf 27, der Zug 1.c4 nur auf 22. Der Zug 1.f3 verringert sogar die Gesamt-Beweglichkeit von 20 auf 19, was aber, wie jeder Schachspieler weiß, nicht der einzige Grund gegen diese merkwürdige Eröffnung ist. Wenn etwa 1...e5 folgt und Weiß im 2. Zug mit 2. g4 „genial“ fortfährt, kann Schwarz ihn bekanntlich mit 2...Dh4 mattsetzen und damit einen Weltrekord in der Kürze der Partie aufstellen.
Nach diesen Vorbereitungen war mir klar, was ich in der Testpartie zu tun hatte. Ich führte mit Schwarz eine Stellung herbei, in der Weiß noch nicht rochiert, wohl aber seine Dame, den Sb1 und den Lc1 schon entwickelt hatte. Während sein b- und c- Bauer schon durch Abtausch „gestorben„ waren, stand der a-Bauer noch brav auf a2 , der Turm tatenlos auf a1, und auch sein g-, f- und h-Bauer standen noch auf ihren Geburtsfeldern. Als es mir dann noch gelang, das Programm zu dem Zug d4xe5 und damit zur Öffnung der d-Linie zu verleiten, wusste ich, dass nun einen Zug später sofort die lange Rochade folgen würde. Dies trat auch prompt ein, denn der Turm gewann ja durch den Rochadeschritt von a1 nach d1 enorm an Beweglichkeit, vor allem in vertikaler Richtung.
Der neben mir sitzende Programm-Autor und sein Chef waren recht betreten, als sie nun zusehen mussten, wie ich den nach der (positionell völlig unsinnigen) langen Rochade schutzlos gewordenen König mühelos angreifen und mattsetzen konnte. Natürlich wurde, als ich fort war, das Programm mit seinen 14 Kriterien sofort verbessert - ein kleiner Schritt in Richtung auf die heutigen Schachprogramme, die z.T. auf Weltmeister-Niveau spielen.
Mir scheint übrigens, das Problem der Gesamt-Beweglichkeit ist auch unabhängig von dieser Computeranwendung interessant, vor allem für den Anfänger. Denn er wird ja zu Recht angeleitet, z.B. Springer und Türme auf Felder zu setzen, wo sie eine hohe Beweglichkeit erlangen. Auf dieser Idee beruht schließlich das Streben nach Zentralfeldern für den Springer und nach offenen Linien für den Turm. Dass dies bei der Zugentscheidung nicht der einzige Maßstab sein kann, lernt man etwas später (siehe die oben beschriebene Partie mit der fatalen, zum Verlust führenden Rochade). Doch sollte man ja bei allem, was man im Leben lernt, zunächst die einfachen allgemeinen Regeln verstehen, bevor man sich den Ausnahmen zuwendet.
Wohl jeder Schachspieler empfindet gefühlsmäßig, dass die unterschiedliche Stärke von Springer, Läufer, Turm und Dame tatsächlich in erster Linie auf ihrer verschiedenen Beweglichkeit beruht. Wie aber lässt sich dieser Begriff zahlenmäßig präzisieren? Dazu müssen wir zunächst nach der Beweglichkeit jeder einzelnen Figur in einer gegebenen Stellung fragen, also danach, wieviele Felder sie von ihrem Standfeld aus erreichen kann. Ich möchte diese Zahl die konkrete Beweglichkeit nennen. Wohl gemerkt: Sie hängt ab a) von der Figur, b) von ihrem momentanen Standfeld und c) von der Stellung. Z.B. hat in der Ausgangsstellung, wie schon erwähnt, für jeden Springer die konkrete Beweglichkeit den Wert 2, während sie für König, Dame, Turm und äufer noch gleich Null ist.
Eine Theorie der konkreten Beweglichkeit wäre äußerst kompliziert, da ja in einer Partie die Zugmöglichkeiten einer Figur meistens durch andere Figuren eingeschränkt werden – durch gegnerische, die z.B. ein Läufer nicht überspringen kann, und vor allem durch eigene Figuren oder Bauern, die man weder überspringen noch schlagen darf, so gerne man das auch manchmal täte, z.B. wenn man dadurch ein Tempo beim Mattangriff gewinnen würde.
Daher tun wir gut daran, das Thema dadurch zu veinfachen, dass wir neben der konkreten die abstrakte Beweglichkeit betrachten. Darunter wollen wir die Anzahl der Züge verstehen, die eine Figur von einem Feld aus machen könnte, wenn die übrigen 63 Felder alle leer wären. Nochmals: Die abstrakte Beweglichkeit hängt nur von der Figur und dem Standfeld ab, nicht von irgend einer Stellung. Beispiel: Nach dem Eröffnungszug 1.d4 beträgt die konkrete Beweglichkeit der weißen Dame 2, die abstrakte dagegen 21. Es ist offensichtlich, dass bei einer Figur die konkrete Beweglichkeit höchstens gleich der abstrakten sein kann und dass sie manchmal – wie in diesem Beispiel – erheblich kleiner ist. (Die besondere, merkwürdige Situation des Bauern in dieser Hinsicht wird am Ende noch unter Punkt 6 erwähnt.)
Im Folgenden wollen wir nun ausrechnen, wie groß für die einzelnen Figuren die abstrakte Beweglichkeit im Durchschnitt ist, d.h. wenn man alle 64 Felder als gleichwertige mögliche Standfelder betrachtet.
1. Der Springer
Am interessantesten ist bei diesem Thema zweifellos der Springer, weil bei ihm die Beweglichkeit mehr als bei jeder anderen Figur vom Standfeld abhängt (Diagramm 1):
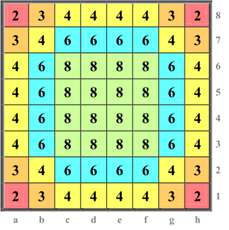
1) Von den (rot zu denkenden) Eckfeldern a1, a8, h1 und h8 aus kann der Springer nur jeweils 2 Felder erreichen, im ersten Fall b3 und c2. Man könnte also in Anlehnung an einen bekannten Vers (siehe Fall 3 unten) dichten:
Springer in den Ecken
sind meistens zum Verrecken.
2) Von den 8 (orange zu denkenden) Feldern aus, die einem Eckfeld waagerecht oder senkrecht benachbart sind, d.h. von a2 , b1, a7, b8, g1, h2, g8 und h7 aus erreicht ein Springer nur ganze 3 Felder (im ersteren Fall b4, c3, c1. Vielleicht passt dazu der Merkvers:
Solang der Springer neben einer Ecke steht,
sieht man sogleich, dass ihm das Spiel fast ganz entgeht.
3) Wenn der Springer auf einem der bisher noch nicht erwähnten (gelb zu denkenden) 16 Randfelder steht (die also weder Ecken noch Nachbarn der Ecken sind, z .B. a3, a4, a5 und a6), dann kann er von dort aus nur 4 Felder erreichen, etwa von a3 aus die Felder b5, c4, c2 und b1. Hier erinnern wir uns an den bekannten Spruch:
Springer am Rande
bringt immer nur Schande.
4) Genau so erreicht der Springer von den 4 (ebenfalls gelb zu färbenden) Fianchettofeldern b2, b7, g2 und g7 aus jeweils nur 4 Felder (im ersten Fall a4, c4, d3 und d1). Gereimt möchte ich das so ausdrücken:
Springer auf dem Fianchettofeld
ist nicht das Beste in der Welt.
5) Besser steht der Springer auf den 16 (blau vorzustellenden) Feldern, die senkrecht oder waagerecht zwischen den Fianchettofeldern liegen, also b3, b4, b5, b6; c7, d7, e7, f7; g6, g5, g4, g3 ; f2, e2, d2, c2. Denn von hier aus kann er jeweils 6 Felder erreichen, z.B. von b3 aus die Felder a5, c5, d4, d2 , c1 und a1.
6) Es bleiben noch die besten („grünen“) 16 Felder des Springers, nämlich das sogenannte große Zentrum. Sie bilden ein 4 x 4 Felder großes Quadrat, dessen Eckfelder c3, c6, f6 und f3 sind. Schon der Anfänger lernt, dass diese Felder für den Springer besonders geeignet sind, weil er von ihnen aus jeweils 8 Felder erreichen kann. Wir sagen das in Versform so:
Der Springer kommt zur vollen Wirkungskraft,
wenn er es in das große Zentrum schafft.
Die mittlere abstrakte Beweglichkeit des Springers, im Folgenden seine MAB genannt, ergibt sich, wenn wir für alle 64 Felder die Beweglichkeiten addieren und die Summe durch 64 teilen. Für diese Rechnung fassen wir immer die Felder zusammen, die im Diagramm die gleiche von den fünf gedachten Farben haben, und zwar in der erwähnten Reihenfolge rot, orange, gelb, blau, grün. Das ergibt nach unseren bisherigen Überlegungen eine Summer aus fünf Summanden, je einen pro Farbe, nämlich
4x2 + 8x3 + 20x4 + 16x6 + 16x8 = 8 + 24 + 80 + 96 + 128 = 336.
Durch die Anzahl der Felder dividiert, erhalten wir 336:64 = 21:4 = 5,25, d.h. im Durchschnitt kann ein Springer in einem Zug 5,25 Felder erreichen. Diesen Wert hat also die MAB des Springers.
2. Der Läufer
Für den Läufer ist die entsprechende Rechnung viel einfacher. Man kann kann unmittelbar Folgendes bestätigen (Diagramm 2):

1) Von jedem der 28 (rot gedachten) Randfelder des Schachbretts aus kann der Läufer jeweils genau 7 Züge machen. (Hier spielen die Eckfelder nur insofern eine Sonderrolle, als bei ihnen alle 7 Zielfelder des Läufers auf der gleichen Diagonale liegen, bei den übrigen Randfeldern dagegen immer jeweils auf zwei verschiedenen Diagonalen.) So kann der Läufer z.B. von c1 aus sowohl die 5 Felder d2, e3, f4, g5 , h6 als auch die 2 Felder b2 und a3 erreichen, zusammen 7 Felder.
2) Stellen wir einen Läufer auf ein Feld wie z.B. b4, das vom Rand durch ein einziges Feld getrennt ist. (Im Diagramm gelb zu denken.) Das sind auf der b-Linie die 6 Felder b2 bis b7, auf der g-Linie die 6 Felder g2 bis g7, zwischen beiden Linien jeweil die 4 Felder in der zweiten und siebten Reihe, also insgesamt 6 + 6 + 4 + 4 = 20 Felder. Auf jedem von ihnen hat der Läufer offenbar die abstrakte Beweglichkeit 9.
3) Wenn der Läufer auf einem Feld steht, das von Rand den Abstand 2 hat (im Diagramm blau zu denken), also auf einem der 12 Felder c3, c4, c5, c6, d6, e6, f6, f5, f4, f3, e3,d3, dann kann er von dort aus jeweils 11 Felder erreichen, z.B. von c4 aus die Felder a2, b3, d5, e6, f7 , g8 sowie auch a6, b5, d3, e2, f1. Hier beträgt seine abstrakte Beweglichkeit also 11.
4) Zu betrachten bleiben nur noch die 4 (grün vorzustellenden) Zentrumsfelder d4, d5, e5, e4. Von hier aus kann der Läufer offensichtlich jeweils 13 Felder erreichen, z.B. von d5 aus die Felder a2, b3, c4, e6, f7, g8 sowie a8, b7, c6, e4, f3, g2, h1.
Die Zahl aller möglichen Läuferzüge, also die Summer aller 64 abstrakten Beweglichkeiten, ergibt sich somit aufgrund einer Rechnung, die der oben für den Springer durchgeführten analog ist, wenn wir wieder die Felder nach Farben zusammenfassen. Wir erhalten
28x7 + 20x9 + 12x11 + 4x13 = 196 + 180 + 132 + 52 = 560.
Die MAB des Läufers beträgt also 560:64 = 35:4 = 8,75 und liegt damit erheblich über der des Springers. Dass trotzdem Läufer und Springer bekanntlich in vielen Stellungen als etwa gleichwertig anzusehen sind, liegt, wie jeder Schachspieler weiß, an anderen Faktoren als der Beweglichkeit. Ich möchte für den Anfänger fünf bekannte Unterschiede zwischen beiden Figuren erwähnen , von denen die drei ersten Vorteile des Springers, die beiden letzten starke Vorteile des Läufers bedeuten.
a) Ein Läufer kann (auch durch noch so lange Zugfolgen) insgesamt nur 32 Felder erreichen, entweder alle weißen oder alle schwarzen. Er bleibt die ganze Partie hindurch an die Farbe gebunden, auf der er „geboren“ ist, z.B. schwarze Felder, wenn sein Geburtsfeld c1 ist, oder weiße im Fall c8. Wer an eine entsprechende Ideologie glaubt, der wird wohl das Schicksal des Läufers als typisch für eine Klassengesellschaft ansehen: Der Ort der Geburt entscheidet über das gesamte spätere Leben. Dagegen kann ein Springer mit einer geeigneten Zugfolge von jedem 64 Felder aus alle Felder erreichen, so dass die Farbe des Geburtsfeldes später keine Rolle mehr spielt. Hierin liegt natürlich ein gewaltiger Vorteil des Springers gegenüber dem Läufer, vergleichbar vielleicht mit den Chancen in einer freien Gesellschaft, wo der Sohn einer armen Putzfrau Bundeskanzler oder sogar Fußball-Millionär werden kann.
b) Ein Läuferschach kann man manchmal dadurch abwehren, dass man eine Figur zwischen den Läufer und den angegriffenen König zieht. Beim Springerschach ist dies unmöglich. Ein weiterer Vorteil für den Springer!
c) Der Läufer braucht im Gegensatz zum Springer in der Eröffnung, um überhaupt ziehen zu können, mindestens einen vorbereitenden Bauernzug. Anders gesagt: In der Ausgangsstellung beträgt die konkrete Beweglichkeit des Springers 2, die des Läufers aber 0. Aufgrund dieser „Frühreife“ kommen in der Partie die Springer meist früher zum Einsatz als die Läufer.
d) Der Läufer kann „große Sprünge“ machen, z.B. von a1 nach h8, was sieben Königsschritten entspricht. Dagegen ist der Springer viel langsamer; denn er bewegt sich immer nur zwei Königsschritte weit (und zwar, um es ganz präzise auszudrücken, zwei solche, deren Richtungen einen Winkel von 45 Grad bilden wie Nord- und Nord-Ost-Richtung). Ein Riesenvorteil für den Läufer!
e) Die beiden Läufer können zusammen wie ein Turm einen Teil des Brettes für den feindlichen König abriegeln. Wenn sie z.B. auf a1 und g8 stehen, können sie den gegnerischen König in das Dreieck mit den Ecken a1, a8 und h8 einsperren. Die beiden Springer können so etwas nicht. So kann man bekanntlich den „alleinstehenden“ König mit zwei Läufern mattsetzen, nicht aber mit zwei Springern. Ein weiterer Vorteil des Läufers - genauer gesagt, des Läuferpaares gegenüber dem Springerpaar.
3. Der Turm
Noch einfacher ist die Rechnung für den Turm, der offenbar von jedem der 64 Felder aus 14 Züge machen kann. Er hat also überall die gleiche abstrakte Beweglichkeit. Daher ist der Mittelwert, also die MAB des Turms, ebenfalls gleich 14. Nur der Vollständigkeit halber sollten wir noch notieren, dass die Anzahl aller denkbaren Turmzüge offenbar 14x64 = 896 beträgt.
4. Die Dame
Um die gleiche Rechnung für die Dame durchzuführen, brauchen wir nur zu bedenken, dass sie von jedem Feld aus genau so viele Züge machen kann, wie die Summe aus der Anzahl der Turmzüge und der Anzahl der Läuferzüge von diesem Feld aus beträgt. Die abstrakte Beweglichkeit der Dame auf einem gegebenen Feld erhält man also immer, indem man die dortige abstrakte Beweglichkeit von Läufer und Turm addiert. Demnach gilt dasselbe auch für die Mittelwerte, sodass sich für die MAB der Dame nach Punkt 2 und 3 der Wert 8,75 + 14 = 22,75 ergibt.
Dieser sehr hohe Wert ist einer der Gründe für die gewaltige Stärke der Dame. Er zeigt zugleich, dass sie schwächer ist als zwei Türme zusammen, auch wenn der Vergleich von 22,75 mit 14 + 14 = 28 irreführend wäre und die Türme stark überschätzen würde. Ein zusätzlicher besonderer Wert der Dame liegt nämlich darin, dass sie von jedem der 36 Nicht-Randfelder aus in acht verschieden Richtungen ziehen und daher häufig mehrere Drohungen gleichzeitig ausüben kann. Oft braucht sie nur einen einzigen Zug, um z.B. die Angriffsrichtung gegen den König von einem Schachgebot zum nächsten um 45 Grad zu ändern. Im Vergleich zu zwei Türmen ist sie daher taktisch flexibler. Man muss unwillkürlich daran denken, dass es Situationen gibt, in denen ein vielseitig Gebildeter mehr leisten kann als zwei einseitig Gebildete zusammen!
Übrigens, die Anzahl aller denkbaren Damenzüge ist gleich der Anzahl aller Läuferzüge plus Anzahl aller Turmzüge, also nach Punkt (2) und (3) 560 + 896 = 1456, was aber für diese für diese Rechnung nicht benötigt wurde.
5. Der König
Auch die Frage nach der MAB des Königs hat einen Sinn insofern, als er ja im Endspiel als Kampf-Figur verwendbar ist (Diagramm 3).
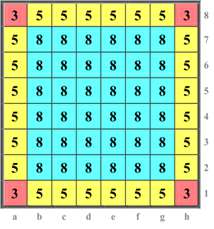
Wir stellen fest, dass der König von jedem der 4 (rot gedachten) Eckfelder aus 3 Züge machen kann, von jedem der übrigen (gelb vorzustellenden) 24 Randfelder aus 5 Züge und von jedem der 36 („grünen“) Nicht-Randfelder aus 8 Züge. Das ergibt nach dem bereits mehrfach angewendeten Muster, dass die Anzahl aller Königszüge (auf dem sonst leeren Brett, wo es natürlich keine Rochade gibt)
4x3 + 24x5 + 36x8 = 12 + 120 + 288 = 420
beträgt, und somit die MAB des Königs
420/64 = 105/16 = 6,5625 ist.
Sie liegt also immerhin über der des Springers, was gewisse Konsequenzen für die Endspieltheorie hat.
Von großer Bedeutung ist die Beweglichkeit des gegnerischen Königs, wenn man ihn mattsetzen will. Denn wir können, etwas unkonventionell, das Ziel definieren als eine Position, in der der gegnerische König im Schach steht und zugleich die konkrete Beweglichkeit 0 hat. Letzteres bedeutet, dass dem König alle „abstrakten“ Fluchtfelder unzugänglich sind (d.h. entweder durch eigene Figuren besetzt oder durch generische bedroht). Daher ist es kein Wunder, dass sich diese Bedingung in der Regel um so leichter herbeiführen lässt, je niedriger die (abstrakte) Beweglichkeit des Königs bereits ist. Die meisten Mattszenen spielen sich auf den roten oder gelben Feldern ab.
6. Der Bauer
Vielleicht fragt jetzt ein Leser, warum wir bisher nicht bei diesen theoretischen Betrachtungen auch die Beweglickeit des Bauern behandelt haben, der ja nicht zu den Figuren gerechnet wird. Der Grund liegt darin, dass der Bauer zu sehr aus dem Rahmen des hier Diskutierten herausfällt (Diagramm 4).
So können Bauern nie in der 1. oder 8. Reihe stehen, weil sie bei ihrer Geburt schon z.B. in der 2. Reihe sind sind und beim Erreichen der 8. Reihe unmittelbar umgewandelt werden. Standfelder von Bauern können also nur die 48 Felder der 2. bis 7. Reihe sein. Die Beweglichkeit eines Bauern beträgt auf dem Geburtsfeld 2, auf den 5 Feldern davor jeweils 1. Insbesondere kann der Bauer auch vom vorletzten Feld, z.B. von c7 aus, einen (in der Regel sehr ersehnten) letzten Zug machen, der zugleich sein Dasein als Bauer beendet und ihn in etwas Höheres verwandelt. Hier drängen sich religiöse Vergleiche auf, die sich jedoch hier nicht weiter erörtern lassen.
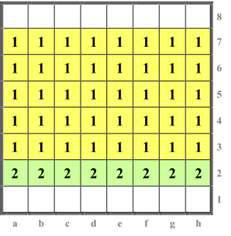
So beträgt die MAB des Bauern offensichtlich 7/6 = 1,1666... Allerdings ist zu bedenken, dass er in einer konkreten Stellung manchmal einen gegnerischen Bauern oder eine Figur schlagen kann. Seine konkrete Beweglichkeit kann daher im Extremfall bis zu 4 betragen, z.B. dann, wenn etwa ein Bauer auf c2 steht und zwischen den 4 Zügen c3, c4 , cxb3 und cxd3 wählen kann. – Im Unterschied zu allen Figuren hat also der Bauer die besondere Eigenschaft, dass seine konkrete Beweglichkeit größer sein kann als die abstrakte.
Um nochmals auf das eingangs erzählte Erlebnis aus den 1960er Jahren zurückkommen: Die Idee mit der Gesamt-Beweglichkeit war sicher nicht das Nonplusultra, nicht der krönende Abschluss im Computerschach. Aber sie war ein guter erster Ansatz, der in der Zwischenzeit enorm weiterentwickelt werden konnte - wie andere Ideen im Leben auch. Man sollte eben etwas Sinnvolles nicht einfach aufgeben, wenn es einmal zu Misserfolgen geführt hat.
Bodo Volkmann